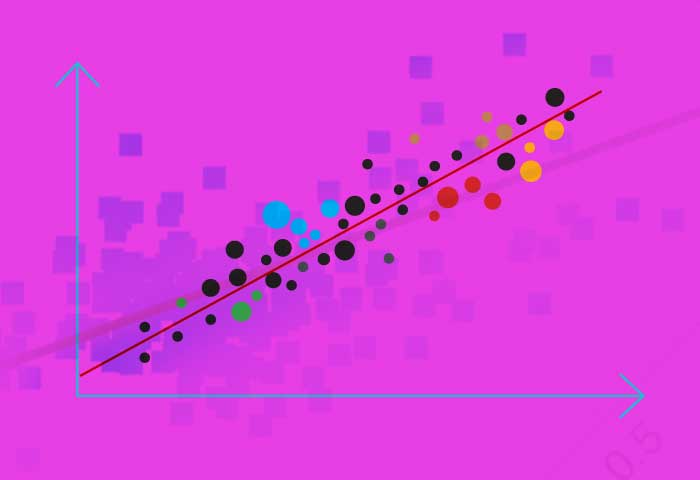
Linear Regression: Understanding Metrics

R-squared

Imagine you're trying to guess how tall your friends will be when they grow up. You might notice that kids who eat a lot of vegetables tend to be taller than those who don't.

Linear regression is like a fancy way to see how strong that connection is. R-squared is a score that helps us understand how good that guess is.

Think of it like a dartboard. The bullseye is where you perfectly predict someone's height based on how much they eat vegetables. The further away from the bullseye your darts land, the worse your guesses are.

High R-squared (close to 1): Your darts are landing really close to the bullseye. There seems to be a strong connection between vegetable eating and height in your friend group.
Low R-squared (closer to 0): Your darts are scattered all over the board. There might not be much of a connection between vegetable eating and height.

R-squared doesn't tell you if eating vegetables makes you taller, but it shows how well your guess about height based on vegetables works for your group of friends. It's like a score for how good your dart-throwing skills are at predicting height!

R-squared answers: How useful was eating vegetable is for predicting height?

P-value

Imagine you're flipping a coin to see if it lands on heads or tails. Normally, it should land on either heads or tails with equal chance, right?

P-value in linear regression is kind of like a surprise test for that coin. We flip the coin a bunch of times (let's say 10) and see how many times it lands on heads.

High P-value (close to 1): The coin seems to be flipping fairly, landing on heads about half the time we expect. In linear regression, this means the observed relationship between variables might just be due to chance, not a real connection.
Low P-value (closer to 0): The coin landed on heads way more than expected (or way less than expected for tails). This is surprising! In linear regression, a low p-value suggests the connection between variables we see is unlikely to be just by chance. It might be a real connection!

Here's the catch: We set a threshold for how surprising the coin flips are before we consider it unusual. Often in science, that threshold is 5%. So, if the p-value is less than 5%, it's like seeing a bunch of heads in a row – that's surprising and suggests a real connection between variables in your regression.

Remember, p-value doesn't tell you exactly what the connection is, just how surprising it is. It's like the surprising coin flips telling you something weird might be going on, but not why.

P-value answers: Was that relationship due to chance?

Adjusted R-squared

Imagine you and your friends are playing a guessing game about how many jellybeans are in a jar. You might each come up with a guess.

R-squared, like we talked about before, is like a score for how close everyone's guesses are to the actual number of jellybeans. But what if you keep adding more and more friends to the game?

R-squared can go up just because there are more guesses. Even if the new guesses aren't very good, they might accidentally get closer to the real number, bumping up the overall score.

Adjusted R-squared is like a special version of the score that considers the number of people playing. It kind of punishes guesses from extra players unless they're truly good.

High Adjusted R-squared (close to 1): Even with more people guessing, everyone's guesses are still really close to the actual number of jellybeans. There must be a strong connection between something (maybe the jar's size?) and the number of jellybeans.
Low Adjusted R-squared (closer to 0): Even though there are more guesses, they're all scattered around. The extra guesses didn't really help, meaning the connection between something and the number of jellybeans might be weak.

So, adjusted R-squared helps us understand how well the model explains the data, considering the complexity of the model (number of variables used for guessing). It's like the original guessing game score, but adjusted to account for how many people are playing!

Adjusted R-squared answers: How well does the model explain the variability in the data, considering the number of variables used?

Mean Squared Error (MSE)

Imagine you're playing darts with your friends, trying to hit the bullseye. Each throw lands somewhere on the dartboard.

Mean Squared Error (MSE) is like a way to measure how far off your throws are from the bullseye, on average. Here's how it works:

Measure the distance: For each throw, you measure the distance between where the dart landed and the bullseye.

Square the distances: Since some darts might land far away and some might be close, squaring the distances makes sure bigger misses are punished more than smaller ones. A big miss far from the bullseye will have a much larger squared distance compared to a small miss close by.

Take the average: Finally, you add up the squared distances from all your throws and divide by the total number of throws. This gives you the average squared distance, which is the MSE.

Lower MSE (closer to 0): Your darts are landing closer to the bullseye on average. This means your predictions in linear regression are very close to the actual values. You're a dart-throwing champion!
Higher MSE (farther from 0): Your darts are scattered all over the place, with some landing far away from the bullseye. This means there's a bigger difference between your predictions and the actual values in linear regression. There's more room for improvement in your dart-throwing (or model)!

Important note: MSE uses squared distances, so even small misses can contribute to the overall error. This is why a lower MSE is better and indicates a more accurate model.

Mean Squared Error (MSE) answers: How much, on average, are the predictions of our model different from the actual values?

Root Mean Squared Error (RMSE)

Root Mean Squared Error (RMSE) is like MSE's (Mean Squared Error) cooler cousin. They both measure how far off your predictions are from the actual values in linear regression, but RMSE presents the answer in a way that's easier to interpret.

Remember the dartboard analogy from MSE? Here's how RMSE builds on that:

Measure and square: Just like MSE, RMSE starts by measuring the distance between each dart throw and the bullseye, then squares those distances to emphasize bigger misses.

Take the average: It adds up all the squared distances from your throws and divides by the total number of throws, just like MSE.

Take the square root: This is the twist! By taking the square root of that average squared distance, RMSE brings the error units back to the same scale as your original data.

Think about it like this: Squaring the distances in MSE can make the errors seem much bigger than they really are. The square root in RMSE undoes that squaring, giving you a more intuitive understanding of the average error.

Lower RMSE (closer to 0): Your darts are still landing close to the bullseye on average, just like with a low MSE. But here, RMSE tells you that distance in the same units you used to measure the dart throws (centimeters, inches, etc.).
Higher RMSE (farther from 0): Your darts are scattered further away, similar to high MSE. But again, RMSE tells you that average distance in the original units.

Why use RMSE over MSE?

While MSE is a good starting point, RMSE is often preferred because:

Easier to interpret: The units of RMSE are the same as your data, making it easier to understand the magnitude of the errors.
Better comparison: If you're comparing models with different scales on the dependent variable, RMSE allows for a fairer comparison.

Here's an analogy:

Imagine you're a carpenter estimating how much wood (in meters) you'll need for a project.

A low RMSE would mean your estimates are very close to the actual wood needed on average (in meters).
A high RMSE would mean your estimates are way off on average, but you know how much you're typically off by (in meters) thanks to RMSE.

So, RMSE is like a more user-friendly version of MSE, giving you a clear picture of the average prediction error in the same units as your data.

Root Mean Squared Error (RMSE) answers: On average, how much are the predictions of our model different from the actual values, in the original units of measurement?

Mean Absolute Error (MAE)

Imagine you're playing darts again, but this time you're not worried about the bullseye – you just want your darts to land close to the dartboard in general. Mean Absolute Error (MAE) is like a way to measure how far off your throws are from the edge of the board, on average, without considering direction.

Here's how it works:

Measure the distance: For each throw, you measure the distance between where the dart landed and the nearest edge of the dartboard.

Take the absolute value: Since you don't care if the dart landed to the left or right of the center, you take the absolute value of the distance. This ensures both overestimates (darts landing past the board) and underestimates (darts landing short) contribute equally to the error.

Take the average: Finally, you add up the absolute distances from all your throws and divide by the total number of throws. This gives you the average absolute distance, which is the MAE.

Lower MAE (closer to 0): Your darts are landing closer to the board on average, regardless of direction. This means your predictions in linear regression are, on average, very close to the actual values, even if they might be a bit off sometimes.
Higher MAE (farther from 0): Your darts are scattered all over, with some landing far away from the board. This means there can be bigger differences between your predictions and the actual values in linear regression. There's room for improvement in your dart-throwing (or model)!

MAE vs. MSE/RMSE:

MAE focuses on the absolute difference, giving equal weight to both overestimates and underestimates.
MSE and RMSE square the errors, making larger errors influence the score more heavily.

So, MAE might be a better choice when:

Large errors are particularly undesirable.
You don't care about the direction of the errors (overestimates vs. underestimates).

Here's an analogy:

Imagine you're a delivery driver estimating how long each delivery will take (in minutes).

A low MAE would mean your estimates are very close to the actual delivery times on average, even if some deliveries take a little longer or shorter than expected.
A high MAE would mean your estimates are often way off, with deliveries taking much longer or shorter than predicted.

MAE gives you a good sense of the average difference between predicted and actual values, regardless of direction. This can be helpful in understanding how well your model performs in real-world scenarios where absolute errors matter more than following a perfect linear fit.

Mean Absolute Error (MAE) answers: On average, how much are the absolute differences between the predictions of our model and the actual values?

How it works

Here's a breakdown of how each metric works in linear regression:

R-squared:

What it does: Measures the proportion of variance (spread) in the dependent variable explained by the independent variable(s) in your model. Higher R-squared indicates a better fit between the model and the data.
How it works:

Calculates the total variance of the dependent variable (how spread out the actual values are).

Calculates the variance of the residuals (errors between predicted and actual values).

Divides the explained variance (difference between total and residual variance) by the total variance and squares the result.

R-squared values range from 0 (no explanation) to 1 (perfect fit).

P-value:

What it does: Indicates the probability of observing a relationship between the variables as strong or stronger than what you see in your data, assuming there's truly no relationship (null hypothesis).
How it works:

Calculates a test statistic based on the model's coefficients and error terms.

Compares the test statistic to a pre-defined probability threshold (often 0.05).

A low p-value (less than the threshold) suggests the observed relationship is unlikely due to chance, hinting at a real connection.

Adjusted R-squared:

What it does: Similar to R-squared, but it penalizes models with more independent variables to avoid overfitting. It reflects the model's ability to explain the data while considering its complexity.
How it works:

Starts by calculating the regular R-squared.

Adjusts the R-squared value by considering the number of independent variables in the model.

A higher adjusted R-squared indicates a better fit while accounting for model complexity.

Mean Squared Error (MSE):

What it does: Measures the average squared difference between the predicted and actual values. Lower MSE indicates a better fit with smaller errors on average.
How it works:

For each data point, calculates the squared difference between the predicted value and the actual value.

Averages the squared differences across all data points.

Root Mean Squared Error (RMSE):

What it does: Similar to MSE, but expresses the error in the same units as the data, making it easier to interpret.
How it works:

Calculates the MSE as described above.

Takes the square root of the MSE to bring the units back to the original scale of your data.

Mean Absolute Error (MAE):

What it does: Measures the average absolute difference between the predicted and actual values. It focuses on the magnitude of errors, without considering direction (overestimates vs. underestimates).
How it works:

For each data point, calculates the absolute difference (without considering positive or negative) between the predicted value and the actual value.

Averages the absolute differences across all data points.

Here's an analogy to remember these metrics:

Imagine you're a baker trying to bake cookies all the same size:

R-squared: How well, on average, do your cookies match your target size (percentage explained by recipe)?
P-value: How likely is it that your recipe consistently produces cookies close to the target size by chance?
Adjusted R-squared: How well do your cookies match the target size considering the number of ingredients in your recipe (complexity)?
MSE: How much do your cookies, on average, deviate from the target size in terms of squared area? (Lower is better)
RMSE: On average, how much do your cookies deviate from the target size in terms of actual diameter? (Easier to interpret than MSE)
MAE: On average, how much do your cookies differ from the target size in terms of absolute diameter, regardless of being bigger or smaller?

Interview POV

Here's how you can answer an interview question about these linear regression metrics in a clear and concise way: